Calculation of an alternative fret position, taking into account the additional tension appearing in the string when it is pressed to the fret.
This calculation is considered in this work, for the musical instrument “arpeggione”.
The data obtained in this work can be adapted to any musical instrument with the equal temperament scale.
When the string is at rest, a tension force acts on the string.
Depending on the diameter of the string, its material, and the tension of the string, it will vibrate at a certain frequency when a finger, pick, or bow is acting on it.
More accurately, it will be the sum of the spectral components – harmonics, known to musicians as – natural flageolets.
In this study, we are interested only in the basic tone. It is the initial parameter for calculating the arrangement of the frets.
Modern musical instruments use an equal temperament scale. It is peculiarity is that the octave is divided into 12 equal semitones.
Increasing the sound of a note by an octave means increasing the frequency twofold. For example: “a1” is 440 Hz, “a2” of the second octave is 880 Hz. The difference in frequency of neighboring semitones is the twelfth root of two.
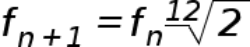
Formula 1
The modern practice of making guitars and other musical instruments with a equal temperament scale uses this principle in calculating the position of the frets. This does not take into account the rigidity of the string. This results in an inaccurate tuning. And, as you move from the first fret to the last fret, this inaccuracy increases.
This work is intended to provide a mathematical way to calculate the position of each fret, taking into account the rigidity of the strings.
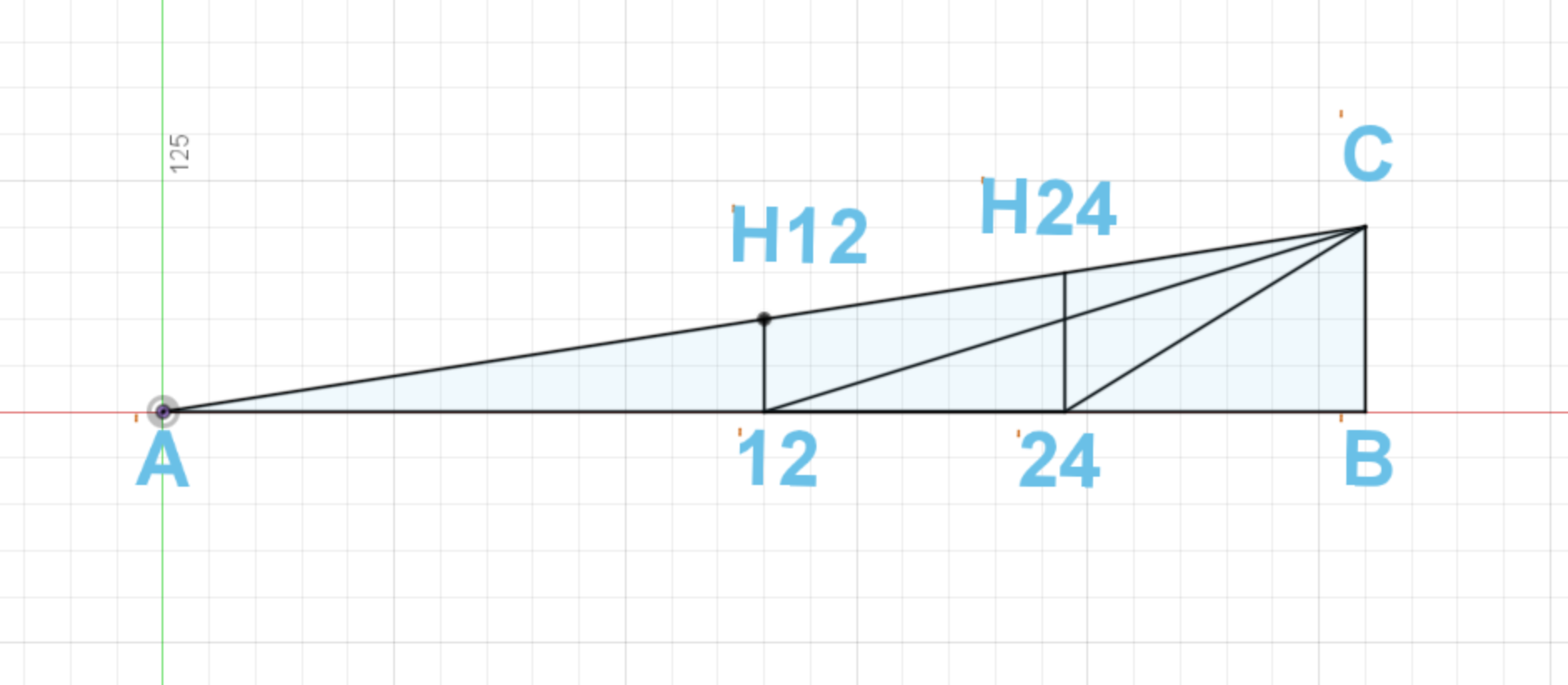
Figure 1 shows the geometry of the string.
AB is the distance from the nut to saddle (or bridge).
AC is the actual length of the string.
12 and 24 are the fret numbers.
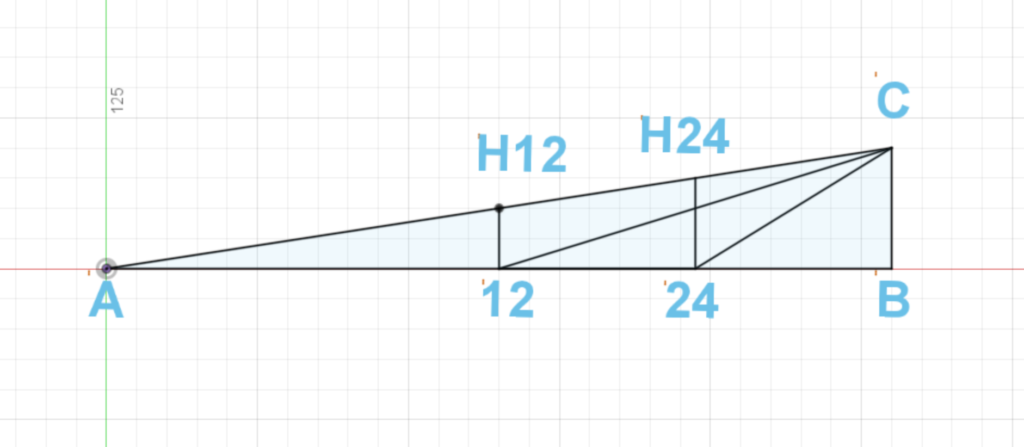
Figure 1. String geometry.
As you can see, the height of the string on the 24th fret is more than on the 12th fret.
When we press a string to a fret, we are acting on the string with some force. This additional force is added to the resting tension force and results in an increase in the vibration frequency of the string. And this force increases as the fret number increases, because the distance from the string to the fret at each successive fret is slightly greater than at the previous one.
In normal guitar fine tuning practice, this extra tension is compensated for once by increasing the length of the string. For electric guitars, it’s tuning with the saddles of each string. For acoustic and classical guitars, it is the displacement of the bridge with the saddle by a certain distance. For guitars with a movable bridge – it is moved all together. Usually this value for the first string is about 2 mm – for the 6th string – about 5 mm.
The thicker and therefore more rigid the string, the greater this additional force.
Consequently, the distance by which you have to move the saddle increases.
Usually for this kind of tuning, you compare the natural harmonic at the 12th fret to the frequency of the string vibrating at the 12th fret. The natural harmonic is free of additional tension. The string pressed at the 12th fret has some additional tension. The saddle is moved to such a length that the oscillation frequency of the natural harmonic and the pressed string are the same.
However, as I said earlier, string height is a value that grows from the first to the last fret.
And we compare it once on the 12th fret.
So the guitar has the exact tuning only on the 12th fret.
It is important to note that this calculation must be done for different types of strings, material and gauge.
However, even with the averaged values, this fret location scheme will be more accurate than the geometrical one that manufacturers use now.
Some tuning error can then be compensated by adjusting the saddle position.

Table 1. String height above each fret.
In my instrument, an arpeggione, I use acoustic guitar strings with a flat wound – D’Addario Flat Tops 0,012 – 0,053.
I use five strings and a lower scale – 5 string – “C” of the great octave, 1 string – «c1» of the one-line octave.
Accordingly, my first string is the second string from the set.
Figure 2: Diameter and tension data provided by the manufacturer.
For a standard scale length – 650 mm
(b1) diameter 0.41 mm, tension – 10.53 kg.
The note “E” of the one-line octave.
The frequency is 246.94 Hz
(E) diameter 1.35 mm, tension – 11.05 kg.
The note “E” of the great octave.
Frequency – 82.41 Hz
Input data for the calculation.
Scale length (l) – 650 мм – 0,65 м
Tension (N)- 10,53 kg- 103,19 Н
Diameter (d) – 0,41 мм = 0,00041 м
Density (ρ) – 7800 kg/м3
The frequency of the string is calculated using the formula.
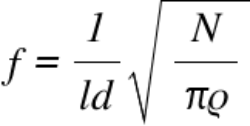
Formula 2
f = 239,7676912 Hz
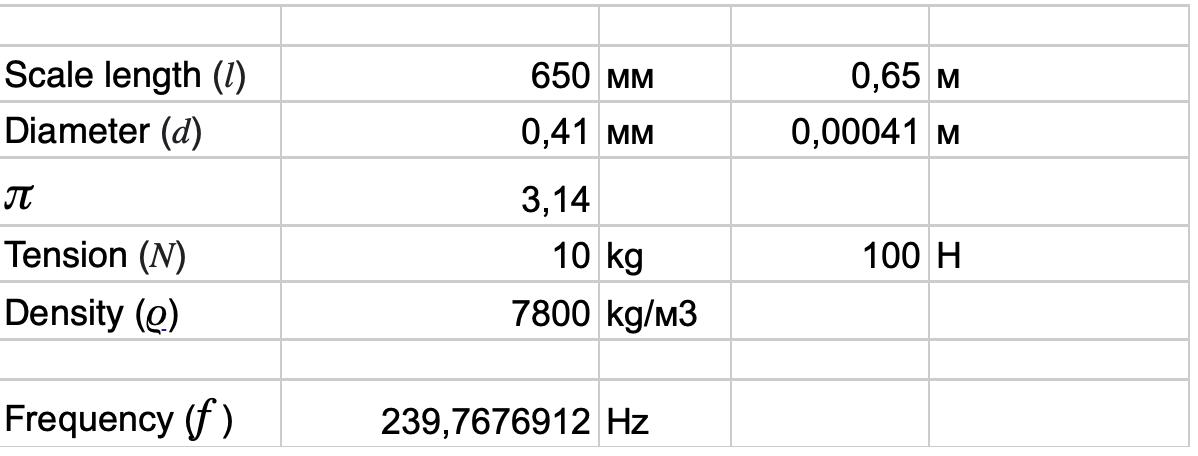
Table 2
We obtained a value slightly different from the tabulated frequency value. The reason for this is that we took the average density value for steel. . A specific string material may have a slightly different density.
The density of the string material should be determined using the inverse formula.
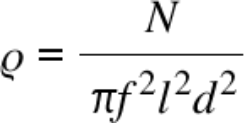
Formula 3
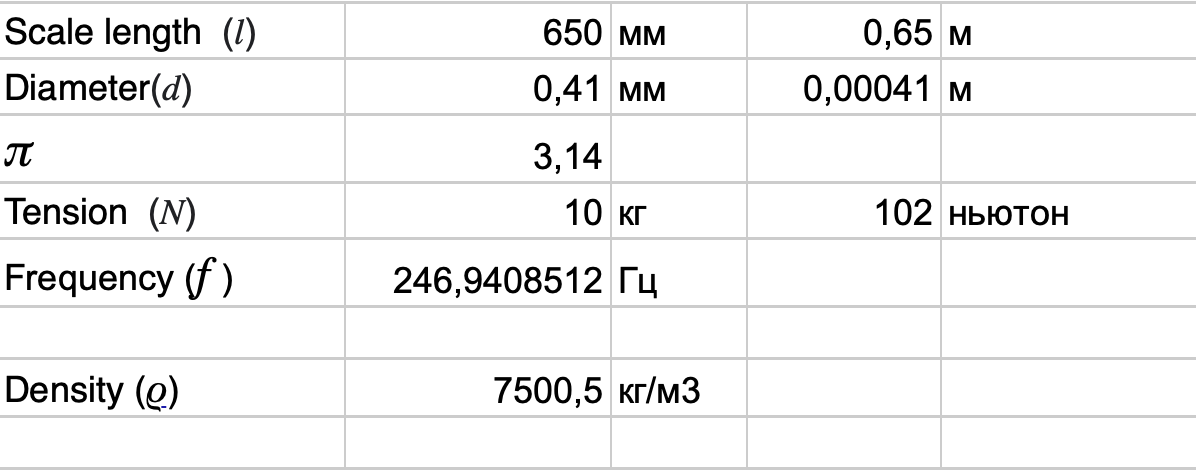
Table 3
We got a value of 7500.6 kg/m3
Now I need to calculate the tension for my note and string length.
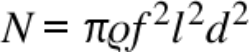
Formula 4
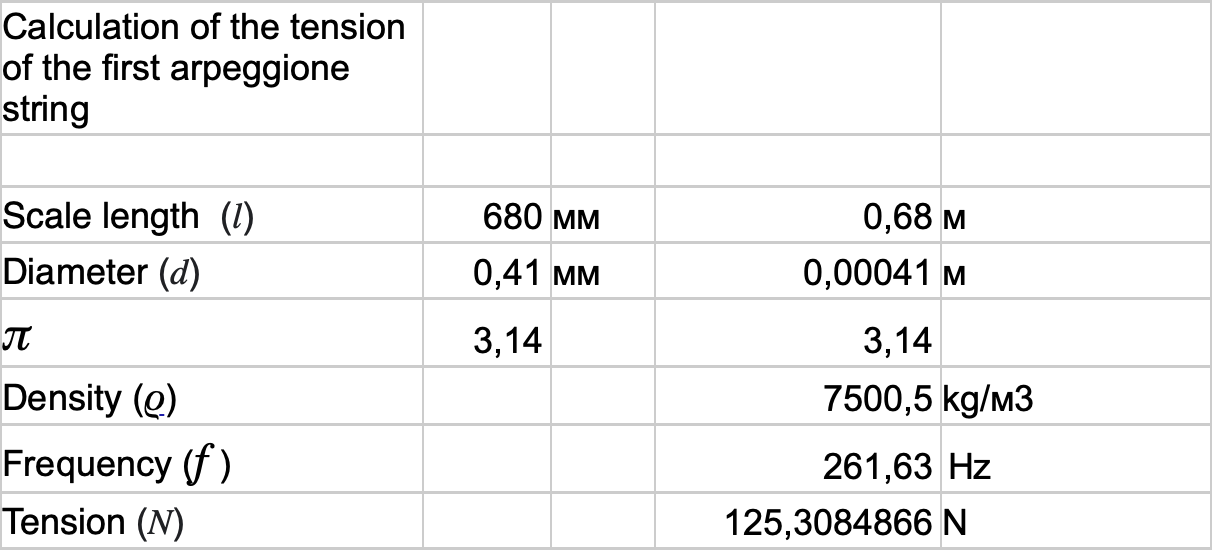
Table 4
The calculation will be made by the theory of flexible thread, taking into account the elasticity of the material.
The formulas are taken from the work of:
https://vestnik.sibadi.org/jour/article/viewFile/352/350
To simplify the calculations, let’s assume that when the string is pressed to the fret, the elongation of the string from nut to fret and from fret to saddle is the same.
In this case we can use the following scheme
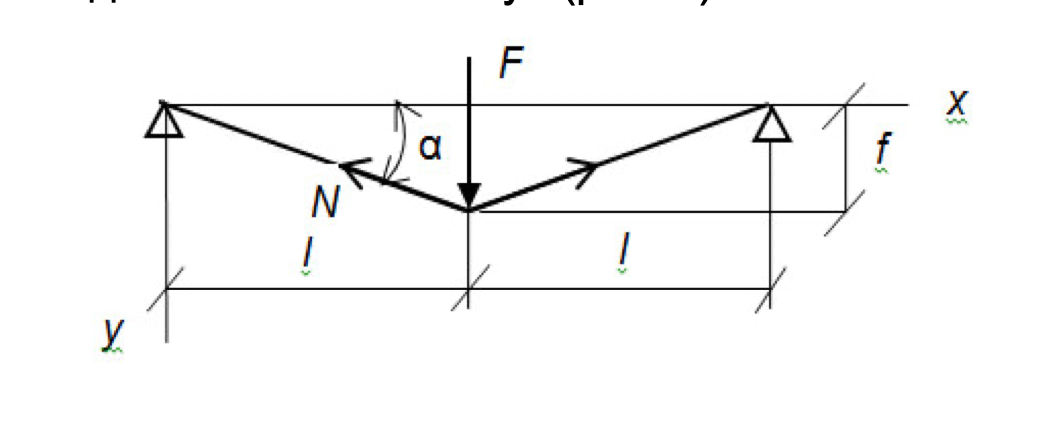
Figure 3. Calculation scheme of the flexible thread.
Elongation of each part of the string with elastic modulus (E), the cross-sectional area (А), the initial tension (N0) and additional tension (N)
The shape that the string takes when it is pressed against the fret is described by a quadratic equation and is shaped like a parabola.
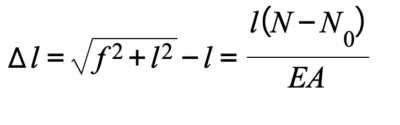
Formula 5
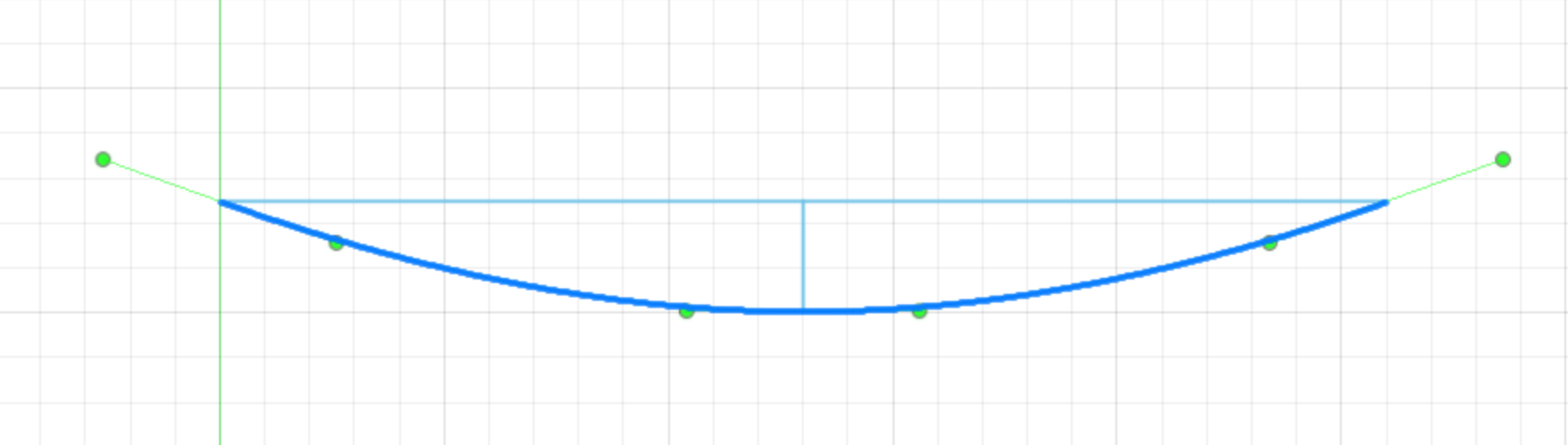
Figure 4
Because of the small movements of the string when it is pressed to the fret, we will make another assumption.
Let’s assume that the string is bent only at the point where it is pressed to the fret and that the parts of the string to the left and right of the fret are a straight line.
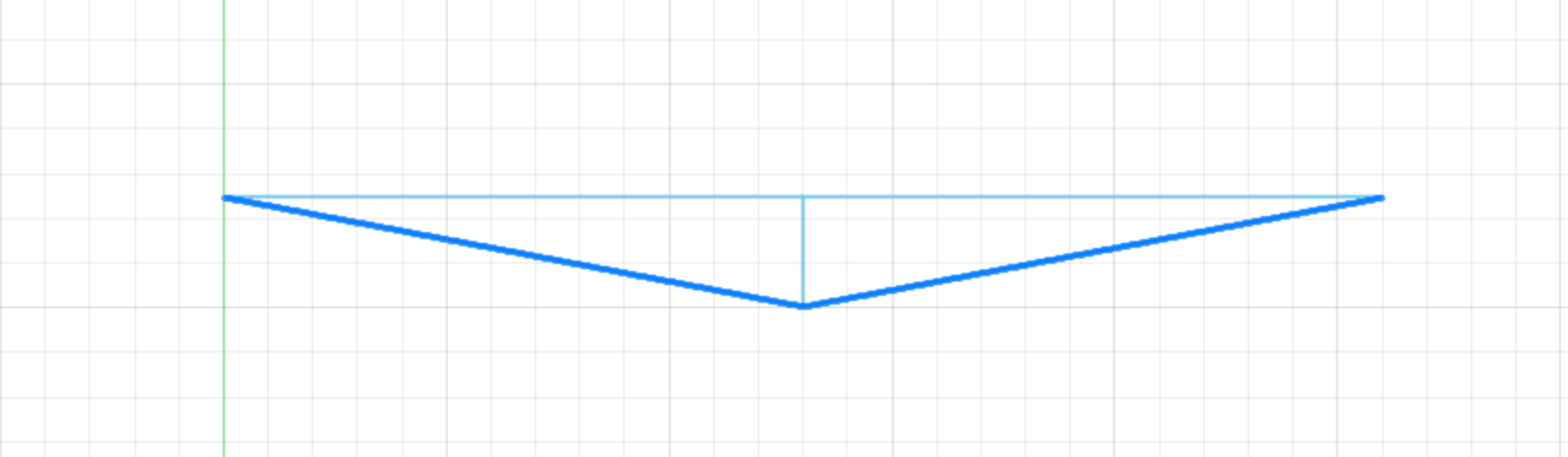
Figure 5

Table 5
Thus, knowing the height of the string above each fret, we can determine the additional elongation of the string when it is pressed against the fret. And knowing the cross-sectional area of the string (A), the initial tension (N0) and the rigidity of the material to calculate the additional tension.
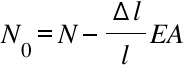
Formula 6

Table 6
Now we can calculate the total tension of the string on each fret.

Table 7. Total string tension, taking into account the tension of the string against the fret.
From this tension, we can calculate the length of string needed to sound at the frequency we want.

Table 8. Estimated length to obtain the tone of the desired frequency.
The results we obtained refer to the real length of the string. This is the hypotenuse of the triangle. (AC). To obtain the values of the fret positions, we need to know the value in the plane of the fingerboard. (АВ).
The table below gives comparative values of the standard fret position calculation of the values obtained in this study. It also indicates the absolute value of the offset of each fret towards the nut.

Table 9. Standard fret placement, estimated fret placement and absolute difference for each fret.
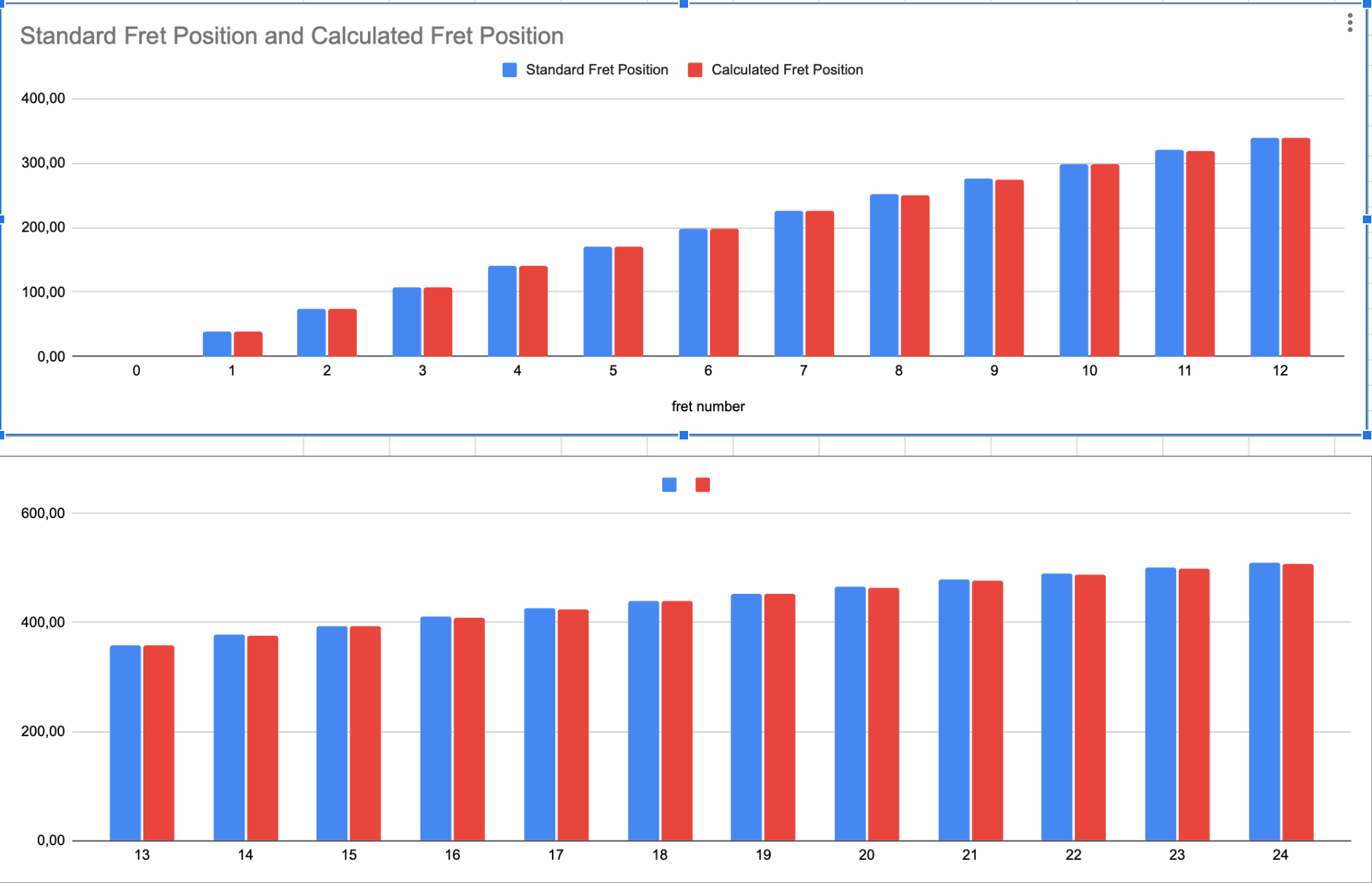
Figure 6
Conclusions:
The calculations show the correctness of the assumption that it is necessary to compensate for the additional tension that occurs in the string when it is pressed against the fret. The results obtained for the 12 and 24 fret shifts correspond to the values obtained in practice for fine guitar tuning.
The calculation is made for 1 arpeggione string – 2 guitar string.
For thicker and more rigid bass strings, the offset will be much larger.
The calculations have an inaccuracy due to assumptions.
1. The modulus of elasticity of the string material is taken as standard for steel. It may vary slightly for a particular string wire material.
2. It is accepted that the bending of the string occurs only at the point of pressure on the fret. Although the string is shaped like a parabola.
3. When the string is pressed against the fret, the string lengthens evenly along its entire length.
4. The distance from the nut to the tuner is not taken into account.
Using this calculation will return the saddle to the calculated scale length.
Some slight inaccuracy of the tuning – due to the physical characteristics of the particular strings used can be compensated for by a slight shift of the saddle or bridge as a whole.
The inaccuracy of the bass strings will be about half as much as with the standard fret position.
This inaccuracy can be corrected by fanning the frets.